Before Pauli postulated his exclusion principle, much of what is now taken for granted about the nature of chemical behavior, was a mystery. Many phenomena, such as the physical indistinguishability of electrons, trends in the periodic table, or the multiplet structure of the atomic spectra, could not be explained by the four quantum numbers alone. Pauli, in 1924, therefore made the following conclusion: The Pauli Exclusion Principle.

To explain what Pauli's principle means in quantum mechanical terms, consider first a two-electron system, e.g. helium. For such an electronic system, Pauli’s principle can be regarded as a property of the wave function: The electronic wave function must be antisymmetric with regard to permutation of the electronic coordinates (i.e. antisymmetric with respect to the exchange of the coordinates of two electrons):

.

If both electrons are assumed to be approximately independent of each other, then the overall wave function can be written as the product of two one-electron functions (orbitals):

.

Taking into account that

1. both electrons are indistinguishable which means that each electron is as likely to be as in as in and
2. the overall wave function must be antisymmetric with respect to exchange of the coordinates (position and spin) of these two electrons,

the following wave function can be constructed from one-electron functions to fulfill these conditions:

.

If both electrons were described by the same set of quantum numbers (a = b) the wave function would become zero, i.e. the wave function vanishes - meaning that no such state exists!

At this point the mathematical foundation of Pauli’s principle becomes clear. Physically, what Pauli's principle means is that

(i) no two electrons with the same spin can occupy the same spatial function (orbital). Therefore, the ground state of a helium atom must include two electrons of opposite spin.

(ii) If electrons occupy a mixture of two different spatial functions, then the can either have the same spin, or opposite spin depending on whether the resultant spatial function is antisymmetric, or symmetric, respectively. The state chosen, in this case, is determined by the so-called exchange integral (See Chapter 2.1). This is positive for an isolated atom resulting in an antisymmetric spatial function and therefore parallel electron spins (Hund's rule). It is negative for a covalent bond.

Extending now the discussion from electrons to other particles in general, the following statement can be made:

[for ].

This leads to the fundamental form of Pauli’s principle:

The Pauli exclusion principle dictates that no two Fermions can be in the same quantum state. This finally leads to the aufbau principle, which is why electrons occupy orbitals of successively higher energy.

To elucidate on how to construct an antisymmetric wave function, consider again the antisymmetric wave function of helium and include the factor 1/ (which retains the normalization condition ) leads to

.

This product is simply the expanded form of a determinant:

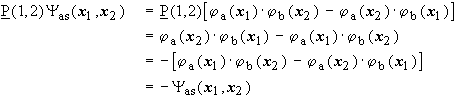
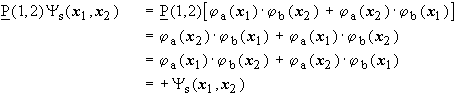
The simplest way to generate an electronic wave function that has the correct antisymmetric properties, is a determinant. An approximate wave function, built from one-electron functions (spin-orbitals), is called a Slater determinant.

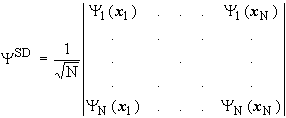
It has proved useful to formulate the orthonormal one-electron functions (spin-orbitals) of an electron as the product of a spatial function (orbital) and a spin function:

.

[ spin orbital, spatial orbital, spin function with a - or b -spin].

Pauli’s principle is introduced by the mathematical properties of a determinant:

The exchange of two electrons (their coordinates) corresponds to the exchange of two columns. The exchange of two columns means a change in the sign of a determinant.

Double occupancy of a spin-orbital (that is, if two electrons possess the same set of the four quantum numbers) results in a determinant having two equal rows. The value of the determinant becomes zero.