with the effective, one-electron Fock operator, 
.
The Coulomb operator (
)
and the exchange operator (
)
are defined by their effect on each arbitrary spin orbital analogues to
the integrals (Jij and Kij):
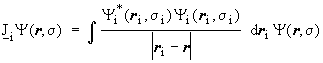
and
.
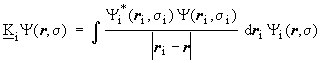A direct solution of the Hartree Fock integro-differential equations
is not possible, since the determined Fock operator depends explicitly
on the functions, 
, obtained.
Such a problem can be solved iteratively by guessing (initial guess)
the first set of starting functions (zeroth approximation). With this first
set of functions, the initial Fock operator, 
,
can be found and can then be used to again solve the HF equations, resulting
in a new set of output functions, 
.
With this new set, the next cycle is started. This iteration will be carried
out until the results for the functions, 
,
and the energies, 
, converge
to within a given error (threshold). This means the HF operator results
in the same functions as those from which the HF operator was determined.
In this case, the result is self consistent and a set of optimized
functions is obtained for the Slater determinant and the energy; the so-called
HF limit. This represents the best solution possible within the independent
electron model. As the HF equations describe the interaction of one electron
with the averaged field of the remaining (n-1) electrons, the term self
consistent field (SCF method) is employed to describe this field
at the HF limit:
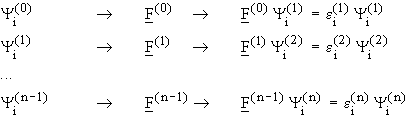
This procedure, the "self consistent field method", was first introduced by W. Hartree in 1927 and applied to atomic problems. In 1930, Fock took antisymmetry into consideration. To honor both this method has been named after them: The Hartree Fock method (which is equivalent to SCF method).
The Hartree Fock equations can be viewed as an alternative Schrödinger equation, where the exact Hamiltonian has been replaced by an approximation, the Fock operator, which describes the interaction with the average field of all the electrons. Therefore, the HF equations appear to be a set of independent equations for each one-electron spin orbital, where the Fock operator itself is a function of the complete set of one-electron spin orbitals.
The eigenvalues, ei, of the HF equations corresponding to the spin orbitals, Y i, are called orbital energies. However, the sum of all orbital energies does not equal the total energy
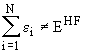
as it would be the case for totally independent electrons! These orbital energies mathematically stem from the Lagrange undetermined multipliers and the sum of the orbital energies is given by
.
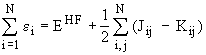According to Koopman’s theorem, the ionization energy, I, can be related approximately to the negative orbital energy of the highest occupied molecular orbital (HOMO). This is a relatively good approximation for at least the first ionization energy. Analogous to the ionization energy, the negative orbital energy of the lowest unoccupied molecular orbital (LUMO) corresponds to the electron affinity, A:
.
Unfortunately, the molecular orbitals describing the resulting cation or anion might well be quite different from those of the neutral, parent molecule, because the electron density might relax (orbital reorganisation). Koopman’s theorem does not account for such effects. Therefore, for ionic systems, additional HF calculation have to be performed. Due to error cancellation, the ionization energy is more accurate than the electron affinity (error addition).
last changes: 01.04.2008, AS questions & comments to: axel.schulz@uni-rostock.de