Coupled Cluster Theory
Pair theory is a physically inspired approach
to incorporating electron correlation. According to Pauli’s
principle, no more than two electrons are allowed to come close to each other,
resulting in the idea that pair correlation must represent the major part of
electron correlation. Pair theory is a particular type of coupled cluster
theory. This theory uses a wave function which can be generally written as a
sum of
where 
describes the
correlation of two, 
of three electrons
etc. This expansion is finite and the series can be calculated recursively from 
. When the expansion is truncated after , this is referred to as pair theory. Pair theory can be
split into several categories, among which are IEPA (independent electron-pair approximation) and CEPA (coupled electron-pair approximation),
which is also known as CCD (coupled
cluster double excitation).[i],[ii],[iii]
First introduced in
nuclear physics,[iv] this
approach was adapted for the molecular problem by Cizek.[v]
This method satisfies the size-consistency condition, but like the MP method, not variational. It offers
a better approximation than perturbation theory, if
the correlation correction is large (i.e. large perturbation means that the MP
method becomes unreliable).
Starting with the HF reference wave function
(in the ground state), the CC procedure is based on the exponential ansatz :
,
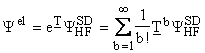where 
is the
cluster
operator of a N electron-containing system:
and the individual members are defined as follows:
analogous
to triple substitutions.
In these expressions, the indices, i, j, k, l,..., characterize occupied spin-orbitals
and r, s, t, u, .... virtual spin-orbitals.
Introducing substitution operators, e.g. for a double
substitutions (
), which are defined by their influence on the HF wave
function (
=
if the HF determinant is the reference):
.
Here, 
corresponds to a
"doubly-excited" single-determinant function in which the
spin-orbital, i (j), is substituted by the virtual
spin-orbital, r (s). The operator, , is antisymmetric in both (ij) and (rs).
In a CC calculation,
the a-coefficients, which control the degree of orbital substitution, have to
be determined. From these coefficients, the wave function and the energies can
be derived. If the wave function of the Schrödinger equation is substituted for
the above exponential expansion, equations which allow the determination of the
coefficients are derived. However, the derivation is non-trivial and the
resultant equations are both complex and non-linear.
In practice, the CCD
method is most commonly applied. This method uses a wave function containing
all possible double excitations.[vi] This is mathematically achieved by
approximating the cluster operator as:
,
so that the wave function can be expressed as
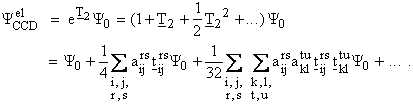
The product of the operators, 
, is treated as zero, if any of the eight indices are
identical. If not, it leads to a quadruple substitution and becomes:
The equations for the a-coefficients are obtained by projection of 
:
onto the function and
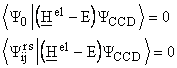and finally
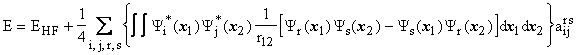
These equations are sufficient to determine the energy, E, and the
unknown a coefficients. Due to the quadratic term, 1/2
, this system contains coupled, non-linear equations which
can be solved iteratively. Neglecting this quadratic term leads to an
approximation known as the linear CCD
method (LCCD), or CEPA, according to the degree of approximation applied to
the quadratic terms. The coupled cluster method is
rapidly becoming a more important technique in computational
chemistry. The CCSD
[vii]
(coupled cluster including single and double substitutions) has been now
extensively compared with CI for energies, equilibrium structures and infrared
intensities in a variety of molecules. Results obtained indicate the
superiority of CCSD over the CISD method. It is assumed that size consistency
plays an important rule. Like CISD, the CCD and CCSD methods
do not adequately
account for triple substitutions. Some approximate treatments, which include
triple terms have been introduced [CCSD(T)].[viii],[ix]