Møller-Plesset Perturbation Theory
A different approach to electron correlation has become very popular in
recent years: The Møller- Plesset method.[i]
Here, higher excitations are taken into account by a
perturbation operator (
) within the many body
perturbation theory introduced by Rayleigh and
Schrödinger. The HF problem is treated as the unperturbated
wave function and the residual part of the Hamiltonian is treated as a
perturbation:
.
The application of the perturbation theory is justified,
if the
contribution of electron correlation energy (the "perturbation“) is small.
This is usually the case. The conditions are:
1) From
the HF computation, the energy eigenvalues and eigenfunctions are known (corresponding to the solution of
the unperturbated system with 
, 
(HF Slater
determinant) and 
):
.
2) If
the perturbation is small, then and lie close to the exact
wave function,
and the energy,
E.
Assuming these two conditions, a generalized electronic Hamiltonian (
) can be defined as:
.
Expanding the wave function (
) and energy as a power series:
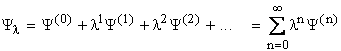
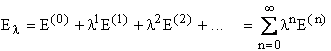
where l is an arbitrary parameter, to keep
track of the orders of perturbation applied.
and
El represent the exact or full CI
(within a given basis set) ground state wave function and energy for a system
described by the Hamiltonian, 
. Note that for = 0, equals the unperturbated operator (0th power) 
.
The following eigenvalue
equation now has to be solved:
.
Substituting the wave function and energy by the power series:
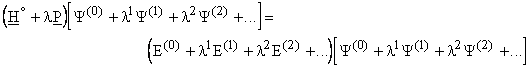
Expanding the products and collecting like terms of l together and equating them (since l is arbitrary) the energies setting l = 1, are given by
, ... .
All resulting terms can be expressed in terms of 
and the determinable term 
. The unperturbated, ground state
wave function and energy can be written in terms of the occupied, one-electron
spin orbitals,
, and the energy of any single spin orbital, ei.
.
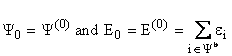Møller
and Plesset introduced the following expression for
the perturbation operator:
.
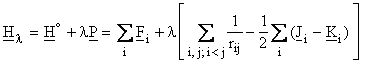E(0) is the sum of the one-electron energies and
therefore, only the sum E(0) + E(1)
represents the HF energy since
Y(0) corresponds to the HF wave function.
To calculate 
the first order wave
function 
has to be known. This
is given by:
.
The energy, 
, corresponding to a determinant, 
, is the sum of one-electron energies of those spin-orbitals which are occupied. 
are
the matrix elements of the perturbation operator. It can be shown that does not become zero,
if s corresponds to a determinant with double substitutions. Thus only double
substitutions contribute to the first order wave function.
Due to the good cost (CPU time) to accuracy
ratio, the power expansion is often truncated after the
second order, known as MP2 level, for which the energy is:
.
The energy (
are spin orbitals; where indices, i and j, correspond to the occupied spin orbitals, 
, and indices, r and s, correspond to the unoccupied spin orbitals, 
) is given by:
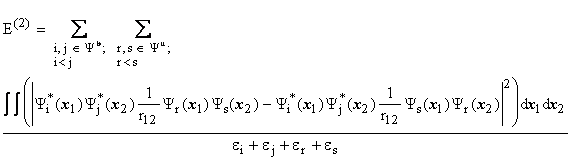
The third order energy,
like MP2 only incorporates
contributions from double substitutions.[ii],[iii]
At MP4 level alone, are additional single, double, triple (MP4 SDT)and
quadruple (MP4 SDTQ) substitutions included.[iv],[v] The MPn method is size-consistent, but not variational. Its principle deficiency is that MP series
sometimes converges slowly, especially in systems where the effects of
correlation are large (corresponding to a large perturbation). The MP method is
practical to fourth order, however, it is limited to
relatively small systems at MP4 level. The MP2 method has been used extensively
even for larger systems. In practice, MP2 must be used with reasonable basis
sets (e.g. 6-31G* or better). Subsequent MP3, MP4 and MP5 are more complicated
and much more time-consuming.
To save CPU time and disc space, MP
computations are often carried out with a
frozen
core (FC) which indicates that correlation effects on the total energy of
the inner-shell electrons are excluded from calculation. That is, only
valence-shell electrons are considered in the electron-correlation computation.
This procedure utilizes the fact that only valence electrons take part in
chemical bond formation. In contrast to a frozen core computation, a
calculation where all electron correlations are included is called a full MPn
calculation.