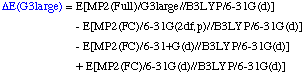G3//B3LYP Theory

G3B3 (or G3//B3LYP) is a variant of G3 theory in which structures and zero point vibrational energies
are calculated at the Becke3LYP/6-31G(d) level of theory. This is particularly advantageous for larger
systems and for open shell systems showing large spin contamination. The G3//B3LYP energy at
0 degrees Kelvin. E₀(G3B3) is defined as:

The definition of the components being:

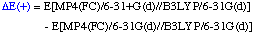
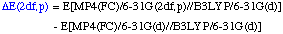
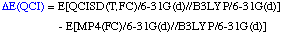
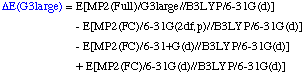
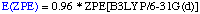
The necessary energies can be calculated most efficiently in the following sequence:

Optimization and frequency calculation at the B3LYP/6-31G(d) level of theory
QCISD(T,FC)/6-31G(d)//B3LYP/6-31G(d) single point
MP4(FC)/6-31+G(d)//B3LYP/6-31G(d) single point
MP4(FC)/6-31G(2df,p)//B3LYP/6-31G(d) single point
MP2(Full)/G3large//B3LYP/6-31G(d) single point

Comments:

Open shell systems are treated using unrestricted Kohn-Sham orbitals (UB3LYP)
The higher level correction (HLC) is supposed to compensate remaining deficiencies
of the method. As in G3 theory, separate values for parameters A and B have been
optimized for atoms and molecules to give the smallest average absolute deviation
from experiment.
Spin orbit correction terms E(SO) (mainly of experimental origin) are added only for atoms.
The mean absolute deviation for the extended G2 neutral set (148 reaction energies)
is 0.93 kcal/mol.

Literature:

L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov, J. A. Pople,
"Gaussian-3 (G3) theory for molecules containing first and second-row atoms"
J. Chem. Phys. 1998, 109, 7764 - 7776.
L. A. Curtiss, K. Raghavachari,
"G2 Theory"
The Encyclopedia of Computational Chemistry, P. v. R. Schleyer (editor-in-chief),
John Wiley & Sons Ltd, Athens, USA, 1998, 2, 1104 - 1114.
A. G. Baboul, L. A. Curtiss, P. C. Redfern, K. Raghavachari,
"Gaussian-3 theory using density functional geometries and zero-point energies"
J. Chem. Phys. 1999, 110, 7650 - 7657.

last changes: 01.04.2008, AS
questions & comments to: axel.schulz@uni-rostock.de