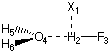The Basis Set Superposition Error (BSSE)
Interaction energies between two atoms or molecules A and B are typically calculated
as the energy difference between the product complex AB and its components A and B:
Eint = E(AB,rc) - E(A,re) - E(B,re)
(1)
The label rc is used here to indicate the geometry of the product complex AB,
while re indicates the geometry of the separate reactants. The interaction
energies calculated according to equation (1) are often too large and lead
to severe complications for systems bound through dispersion interactions or hydrogen bonds.
The helium dimer is a particularly interesting example of the former situation. Using a selection
of different single-reference methods and basis sets of variable size the following results
are obtained:
| method | BF(He) | rc
[pm] | Eint
[kJ/mol]
|
|---|
| RHF/6-31G | 2 | 323.0 | -0.0035
| | RHF/cc-pVDZ | 5 | 321.1 | -0.0038
| | RHF/cc-pVTZ | 14 | 366.2 | -0.0023
| | RHF/cc-pVQZ | 30 | 388.7 | -0.0011
| | RHF/cc-pV5Z | 55 | 413.1 | -0.0005
| | | |
| | MP2/6-31G | 2 | 321.0 | -0.0042
| | MP2/cc-pVDZ | 5 | 309.4 | -0.0159
| | MP2/cc-pVTZ | 14 | 331.8 | -0.0211
| | MP2/cc-pVQZ | 30 | 328.8 | -0.0271
| | MP2/cc-pV5Z | 55 | 323.0 | -0.0317
| | | |
| | QCISD/6-31G | 2 | 320.6 | -0.0042
| | QCISD/cc-pVDZ | 5 | 308.6 | -0.0165
| | QCISD/cc-pVTZ | 14 | 330.9 | -0.0226
| | QCISD/cc-pVQZ | 30 | 326.4 | -0.0309
| | QCISD/cc-pV5Z | 55 | 319.3 | -0.0381
| | QCISD/cc-pV6Z | 91 | 319.3 | -0.0
| | | |
| | QCISD(T)/cc-pVTZ | 14 | 329.9 | -0.0237
| | QCISD(T)/cc-pVQZ | 30 | 324.2 | -0.0336
| | QCISD(T)/cc-pV5Z | 55 | 316.2 | -0.0425
| | QCISD(T)/cc-pV6Z | 91 | 309.5 | -0.0532
|
|
|
He - - - - - - He |
These results have to be compared to the best experimental/theoretical estimates
of rc = 297 pm and Eint = -0.091 kJ/mol.
At the RHF/6-31G(d) level a weakly bound minimum can be identified at interactomic distances
larger than 300 pm. It is remarkable to see how the interaction energy becomes smaller and
the He-He distance larger as the size of the basis set is increased. The underlying reason for
the worsening of the results with increasing basis set size is that the intrinsically bad
description of the dispersion interaction is compensated for by using a small basis set. Small
basis sets stabilize the complex more than the separate components due to the
basis set superposition error (BSSE). The latter is due to the fact that the wavefunction
of the monomer is expanded in much less basis functions than the wavefunction of the complex. In
the latter each of the helium atoms has a larger number of basis functions available than in the
monomer, leading to a more flexible description of the wavefunction and ultimately a lower energy.
One obvious solution to the basis set superposition error is the use of extremely large basis sets.
This is, however, hardly feasible for most of the chemically interesting systems. The second
approach termed the Counterpoise Method (CP) is an approximate
method for estimating the size of the BSSE. While the description of the product complex is
unchanged in the CP method, the separate components are provided with a basis set of identical
size as is available to the dimer. The CP corrected interaction energy can in the simple most case
then be computed as:
Eint = E(AB,rc)AB - E(A,re)AB - E(B,re)AB
(2)
The superscripts AB indicate here that the complex as well as the separate components
are calculated in the same absolute basis. In the helium example discussed before, this
implies that the energies of single helium atoms are calculated in the basis of the dimer
complex. In practice this can be achieved by using the structure of the optimized complex
and resetting some of the nuclear charges of the overall systems with the
Massage keyword:
#RHF/6-31G scf=tight Massage
energy of helium in the basis set of the helium dimer
0 1
He1
He2 1 r2
r2=3.230
1 Nuc 0.0
| |
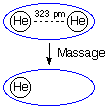 |
In this particular example the RHF/6-31G structure of the helium dimer with an
internuclear distance of 323 pm is used. The Massage keyword
requires additional input as to which atom will be manipulated. Here we reset the
nuclear charge of atom 1 to 0.0. On setting up the calculation Gaussian first
includes all atoms and all basis functions, then assigns nuclear charges and electrons.
The effect of Massage sets in after the basis functions
have been assigned. Resetting the nuclear charge of one of the helium atoms to 0.0 leaves
behind the basis functions positioned at this center in the previous step. These latter
functions are usually referred to as ghost orbitals.
The energy of helium is significantly lower when computed in the full basis of the
complex at -2.85516439247 au as compared to the basis of a single helium atom at
-2.85516042615 au, leading to an energy stabilization of each of the separate
helium atoms by 0.00104 kJ/mol. Calculation of the interaction energy with these
CP corrected monomer energies according to equation (2) gives a reduced
interaction energy of only -0.0017 kJ/mol. Please also note that methods based
on density functional theory are badly suited for the description of weakly bound
systems such as the helium dimer. One further technical note: in some versions of
Gaussian the Massage keyword only works properly
when used in combination with the INDO guess.
The effects of increasing the basis set size are somewhat different when correlated methods
are being used. This is due to the fact that the correlation energy is usually larger in the
complex as compared to the monomers and that an incomplete recovery of the correlation
energy therefore weakens the complex. This effect thus counters the BSSE effect and
the final outcome of increasing the basis set size is not as obvious as in Hartree-Fock
theory.
larger systems
For larger systems such as the hydrogen bonded complex between water and hydrogen fluoride,
the additional question arises as to where to position the ghost orbitals. This becomes problematic
once the structures of the monomers change substantially on dimer formation. In
this situation there is no unique way of placing the ghost orbitals. Formal dissection of the complex
formation process in two separate steps offers a solution to the problem:
(a) deformation of the components A and B from their equilibrium structures to
those assumed in the complex (re to rc).
(b) formation of complex AB from the deformed components.
The CP correction as defined in equation (2) covers both steps even though there
is no reason to assume that step (a) would require such a treatment. A modified formula
for calculation of a CP correction would therefore be:
Eint,cp = E(AB,rc)AB - E(A,rc)AB - E(B,rc)AB + Edef
(3)
with Edef = [E(A,rc) - E(A,re)] + [E(B,rc) - E(B,re)]
The deformation energy Edef is that described by step (a) above and is performed in the monomer
basis only, while all other energy terms in formula (3) are calculated in the full basis of the dimer. The
following input file provides the structure for the H-F/H2O system as optimized at the
HF/6-31G(d) level of theory:
#P HF/6-31G(d) opt=Z-Matrix
HF/6-31G(d) opt H2O/HF complex
0 1
X1
H2 1 1.
F3 2 r3 1 90.
O4 2 r4 1 a4 3 180.
H5 4 r5 2 a5 1 d5
H6 4 r5 2 a5 1 -d5
r3=0.92150424
r4=1.80289277
r5=0.94849694
a4=97.1802224
a5=115.11027415
d5=117.81295527
| |
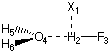 |
The following results are obtained for this system:
| method | r(2-4)
[pm] | Eint
[kJ/mol] | Edef
[kJ/mol] | Eint,cp
[kJ/mol]
|
|---|
| HF/STO-3G | 167.4 | -31.4 | +0.21 | +0.2
|
| HF/3-21G | 161.5 | -70.7 | +1.42 | -52.0
|
| HF/6-31G(d) | 180.3 | -38.8 | +0.4 | -34.6
|
| HF/6-31G(d,p) | 181.1 | -37.9 | +0.4 | -33.4
|
| HF/6-31+G(d,p) | 180.2 | -36.3 | +0.5 | -33.0
|
At the Hartree-Fock level it can clearly be seen that the counterpoise correction
becomes smaller with increasing basis set size. The system chosen here is still
on the small side and the deformation energy Edef as well as the absolute
magnitude of the counterpoise correction are rather small provided that a medium to
large basis set is used. It can also be clearly seen that the use of minimal basis sets
such as STO-3G or 3-21G does not lead to meaningful predictions for two reasons:
(1) the CP correction as calculated by equation (3) is so large that it is similar
in magnitude to the interaction energy itself; combination of the two does not lead
to a reliable prediction of the complexation energy.
(2) the structure of the complex is rather different from that calculated with larger
basis sets, usually leading to complexes, which are somewhat too compact. This implicates
that even a single point strategy based on these structures is doomed to fail!
For a short summary of the BSSE click here.
last changes: 01.04.2008, AS
questions & comments to: axel.schulz@uni-rostock.de