1.
Introduction
Each molecular orbital (one electron
function) yi is expressed as a
linear combination of n basis functions Fm. By convention, molecular
orbitals are abbreviated by the greek letter y (psi), while the basis functions are symbolized by the greek letter F (phi).
![]()
The coefficients cmi are called molecular orbital expansion coefficients or
simply MO coefficients. Usually these
basis functions are located at the center of atoms and are therefore often
called atomic basis functions. This is, however, not strictly true and in order
to avoid confusion, we will in the following use the term basis
function.
The basis functions used in
molecular orbital calculations are usually described through an abbreviation or
acronym such as "6-31G(d)". The complete description of the
theoretical model used in MO calculations is given in the format "theoretical
method/basis set". A calculation using Hartree-Fock theory in
combination with the 6-31G(d) basis set
would then be referred to as "HF/6-31G(d)". Often the molecular
geometries are optimized at one level of theory (method 1) and relative
energies are then recomputed using these geometries, but a different
theoretical method (method 2). The conventional description of this level of
theory is "method
2//method 1". If, for example, geometry optimization has been
performed at the HF/6-31G(d) level of theory and relative energies have then
been calculated at the MP2/6-31G(d) level, this approach would be described as
"MP2/6-31G(d)//HF/6-31G(d)".
In principle, any mathematical
function can be used to construct molecular orbitals. There are, however, only
a few solutions, which have found widespread application.
1.1 Slater type orbitals (STOs)
STOs are constructed
from a radial part describing the radial extend of the orbital and an angular
part describing the shape of the orbital (equ. 3).
![]()
The radial part rn-1 exp(-zr) depends on the distance r
from the origin of the basis function (usually the location of the nucleus),
the orbital exponent z (greek: zeta),
and the principal quantum number n. The spherical part Ylm depends on the angular quantum number l and the magnetic quantum number m. The normalization constant N is chosen such that the integral over
the square of the basis function yields unity. Taking a 1s orbital as an
example, the spherical part as well as the rn-1-factor equate to
unity and after evaluating the normalization constant, we get:
![]()
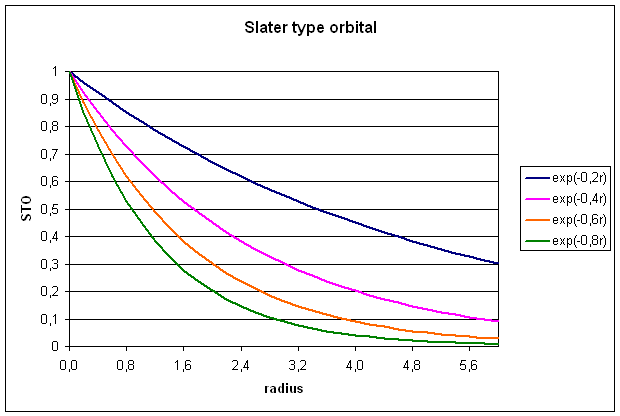
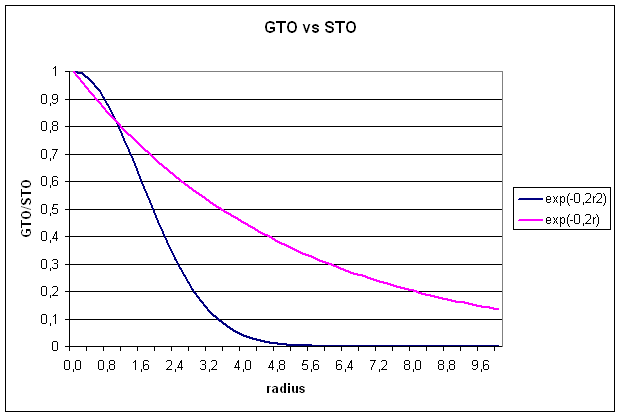
Slater type
orbitals are not very useful for electronic structure calculations, because two
electron integrals over STOs are difficult to calculate.
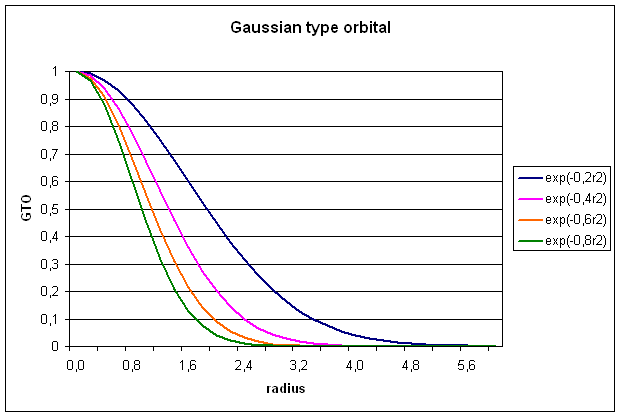
1.2 Gaussian type orbitals (GTOs)
GTOs are also
constructed from a radial and a spherical part, but the radial part now has a
different dependence on r (equ. 5):
![]()
The radial extend
is proportional to exp(-ar2), a being the exponent. The
normalization constant N serves a
similar purpose as for STOs. The spherical part is now expressed through the
cartesian coordinates x,y, and z in powers of a, b, and c, respectively. The exponents a, b, and c, should not be confused with quantum
numbers. The sum of these exponents L=a+b+c is used to define the
angular momentum of the basis functions:
s-type (L=0),
p-type (L=1), d-type (L=2), f-type (L=3), g-type (L=4) . . .. For a
simple Gaussian function representing an 1s-type orbital, we get:
![]()