Mulliken Population Analysis
Directly following the output of molecular orbital
information Gaussian
prints a Mulliken population analysis. A full Mulliken population analysis is
obtained using pop=full. In this case the molecular
orbital information is followed by the current density matrix D (a n*n matrix
with n = number of basis functions). The matrix elements Di,j are
calculated as the sum of products okci,kcj,k over
all k molecular orbitals. The occupation numbers ok
for single determinant wavefunctions are either 0 (virtual orbital), 1 (singly
occupied orbitals), or 2 (fully occupied orbital), and the molecular orbital
coefficient ci,k is that for basis function i in molecular orbital k.
For formaldehyde (CH2O, C2v symmetry) the following results
are obtained at the HF/STO-3G level of theory:
DENSITY MATRIX.
1 2 3 4 5
1 1 C 1S 2.07173
2 2S -0.22403 0.84547
3 2PX 0.00000 0.00000 0.74263
4 2PY 0.00000 0.00000 0.00000 0.63487
5 2PZ 0.01681 -0.07821 0.00000 0.00000 0.55273
6 2 O 1S 0.01218 -0.00171 0.00000 0.00000 -0.04249
7 2S -0.00751 -0.17656 0.00000 0.00000 -0.01027
8 2PX 0.00000 0.00000 0.82369 0.00000 0.00000
9 2PY 0.00000 0.00000 0.00000 0.15487 0.00000
10 2PZ 0.15078 -0.42873 0.00000 0.00000 -0.58493
11 3 H 1S -0.10842 0.28876 0.00000 0.45096 -0.25196
12 4 H 1S -0.10842 0.28876 0.00000 -0.45096 -0.25196
6 7 8 9 10
6 2 O 1S 2.11060
7 2S -0.46427 2.05057
8 2PX 0.00000 0.00000 0.91359
9 2PY 0.00000 0.00000 0.00000 1.90476
10 2PZ -0.09605 0.55492 0.00000 0.00000 1.02854
11 3 H 1S 0.00892 -0.01948 0.00000 -0.35936 0.11723
12 4 H 1S 0.00892 -0.01948 0.00000 0.35936 0.11723
11 12
11 3 H 1S 0.63094
12 4 H 1S -0.24573 0.63094
| |
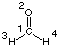 |
As always these results are given with the system in its "Standard Orientation".
The first step in the "Full Mulliken population analysis" involves multiplication of
the density matrix elements Di,j with the corresponding overlap matrix elements
Si,j (again a n*n matrix). In case a basis of normalized, non-orthogonal basis
functions is used, the matrix elements Si,i equate to unity. This implies
that the diagonal elements of the D- and DS-matrices are identical:
Full Mulliken population analysis:
1 2 3 4 5
1 1 C 1S 2.07173
2 2S -0.05564 0.84547
3 2PX 0.00000 0.00000 0.74263
4 2PY 0.00000 0.00000 0.00000 0.63487
5 2PZ 0.00000 0.00000 0.00000 0.00000 0.55273
6 2 O 1S 0.00000 -0.00006 0.00000 0.00000 -0.00260
7 2S -0.00027 -0.06377 0.00000 0.00000 -0.00452
8 2PX 0.00000 0.00000 0.17189 0.00000 0.00000
9 2PY 0.00000 0.00000 0.00000 0.03232 0.00000
10 2PZ -0.00906 0.13729 0.00000 0.00000 0.18336
11 3 H 1S -0.00658 0.13982 0.00000 0.17576 0.06313
12 4 H 1S -0.00658 0.13982 0.00000 0.17576 0.06313
6 7 8 9 10
6 2 O 1S 2.11060
7 2S -0.10990 2.05057
8 2PX 0.00000 0.00000 0.91359
9 2PY 0.00000 0.00000 0.00000 1.90476
10 2PZ 0.00000 0.00000 0.00000 0.00000 1.02854
11 3 H 1S 0.00004 -0.00137 0.00000 -0.01289 -0.00823
12 4 H 1S 0.00004 -0.00137 0.00000 -0.01289 -0.00823
11 12
11 3 H 1S 0.63094
12 4 H 1S -0.03712 0.63094
The example used here illustrates two problems that come up when the DS-matrix elements
are interpreted as atomic orbital occupation numbers. The first problem consists in occupation
numbers larger than 2.0, in clear violation of the Pauli exclusion principle. Second, negative
occupation numbers are clearly unphysical and cannot be interpreted in a classical sense. The
interpretation of single DS-matrix elements is therefore not very meaningful.
Summation of diagonal elements of the DS-matrix together with one half
of all corresponding off-diagonal elements gives the gross orbital populations
for each of the contributing atomic basis functions. That the off-diagonal elements can be distributed
equally among the contributing atomic centers is one of the central assumptions made
in the Mulliken population analysis.
Gross orbital populations:
1
1 1 C 1S 1.99361
2 2S 1.14294
3 2PX 0.91452
4 2PY 1.01871
5 2PZ 0.85523
6 2 O 1S 1.99812
7 2S 1.86937
8 2PX 1.08548
9 2PY 1.91130
10 2PZ 1.32368
11 3 H 1S 0.94352
12 4 H 1S 0.94352
Alternatively, the diagonal and off-diagonal elements can also be summed up for each
of the atoms:
Condensed to atoms (all electrons):
1 2 3 4
1 C 4.736157 0.444580 0.372141 0.372141
2 O 0.444580 7.788268 -0.022449 -0.022449
3 H 0.372141 -0.022449 0.630941 -0.037118
4 H 0.372141 -0.022449 -0.037118 0.630941
Summing up the contributions for each atom and subtracting the nuclear charges gives
the atomic charges (either separately for each atom or with the hydrogen charges
summed up with the adjacent non-hydrogen atoms.
Total atomic charges:
1
1 C 0.074981
2 O -0.187950
3 H 0.056484
4 H 0.056484
Sum of Mulliken charges= 0.00000
Atomic charges with hydrogens summed into heavy atoms:
1
1 C 0.187950
2 O -0.187950
3 H 0.000000
4 H 0.000000
Sum of Mulliken charges= 0.00000
| |
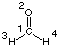 |
Known problems of the Mulliken population analysis include large changes of the computed
atomic charges with small changes in the underlying basis sets and the overestimation of the
covalent character of a bond. These deficiencies can nicely be demonstrated using lithium fluoride
as an example. The following table lists the lithium charge in lithium fluoride as
calculated with the Mulliken population analysis and a variety of Pople basis sets.
The Becke3LYP/6-31G(d) optimized geometry with r(Li-F)=155.139 pm has been used for this
purpose.
| population | basis set | q(Li, RHF) | q(Li, B3LYP)
|
|---|
| Mulliken | STO-3G | +0.227 | +0.078
| | | 3-21G | +0.596 | +0.421
| | | 6-31G | +0.743 | +0.593
| | | 6-31G(d) | +0.660 | +0.526
| | | 6-311G(d) | +0.691 | +0.558
| | | 6-311+G(d) | +0.687 | +0.616
| | 6-311+G(3df) | +0.750 | +0.675
| | | |
| | NPA | 6-311+G(3df) | +0.977 | +0.963
|
| |
Li - F |
While it is comforting to see that the lithium charge is predicted to be
positive with all methods used here, the variation as a function of basis set choice
is rather large (between 0.078 and 0.675 at the Becke3LYP level of theory).
There are, of course, also variations due to changing the Hamiltonian (here from
RHF to RB3LYP), but these appear to be rather constant and comparatively small.
It can also be seen that, even with the largest Pople basis sets used here, the
degree of charge separation between Li and F is underestimated with the Mulliken
population analysis. The Natural Population Analysis (NPA), in contrast, predicts a much
more positive charge on Li.
A detailed overview of the effects of the basis set and the Hamiltonian on the charge distribution
in water can be found in: F. Martin, H. Zipse, J. Comp. Chem. 2005, 26, 97 - 105.
A copy of the pdf file is available here.
last changes: 01.04.2008, AS
questions & comments to: axel.schulz@uni-rostock.de