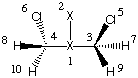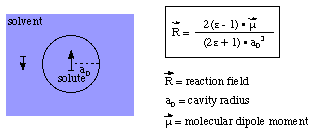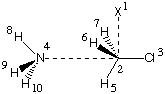Onsager reaction field model

The Onsager Reaction Field Model

The influence between a molecule in solution (the solute) and its surrounding medium (the solvent) can most simply be desribed using the Onsager reaction field model. The basic assumption made in this model is that the solute is placed in a spherical cavity inside the solvent. The latter is described as a homogeneous, polarizable medium of constant dielectric constant. The solute dipole moment induces a dipole moment of opposite direction in the surrounding medium. Polarization of the medium in turn polarizes the charge distribution in the solvent. Treating this mutual polarization in a self consistent manner leads to the Onsager reaction field model as implemented in Gaussian. The reaction field generated in this manner is proportional to the molecular dipole moment and inversely proportional to the third power of the radius of the solute cavity:

The two important properties of this relation are (a) the direct proportionality of the reaction field and the molecular dipole moment, and (b) the inverse proportionality of the reaction field and the third power of the cavity radius. Derivation of the latter is by no means obvious and several different approaches exist. For experimentally well characterized systems with known molar volume, one can obviously divide the molar volume by Avogadro's number to arrive at the molecular volume. Using the simple relation of the radius r of the sphere and its volume V = 4/3*.pi.r³ one can also equate a known molecular volume with the radius of a spherical cavity. Most systems under study are, of course, far from spherical, casting serious doubt on the usefulness of this approach. Also, this approach is rather unpractical as it would limit solvent effect studies to experimentally well characterized cases. One much more practical approach consists in calculating the molecular volume as defined through the contour of constant electron density (e.g. at the value of 0.001 electrons/bohr³), scaling this volume by 1.33 to account for systematic differences between calculated volumes and experimentally measured molar volumes, equating this (non-spherical) molecular volume to the radius of an (ideally spherical) cavity, and adding a constant increment for the closest possible approach of solvent molecules (e. g. 50 pm). This latter approach is used in Gaussian when the volume keyword is being used. This indicates that the cavity radius is nothing else but a freely adjustable parameter that defines, how the solvent reaction field is coupled to the molecular dipole moment. It can thus also be used to adjust the theoretically calculated solvent effect to known experiments.

The results obtained from Onsager reaction field calculations will in the following be illustrated using the gauche- and trans-conformers of 1,2-dichloroethane as an example. It is known from experiments that the energy difference between these conformers is quite sensitive to the polarity of the surrounding solvent, the trans- conformer being favored in a low polarity medium and both isomers being almost isoenergetic in more polar media.

medium	dielectric constant	E(gauche)-E(trans) [kJ/mol]
vapor	1.00	+7.10
cyclohexane	2.023	+4.77
diethylether	4.335	+2.93
acetone	20.7	+1.25
acetonitrile	36.64	+0.98

We start our studies with the C₂ symmetric gauche-conformer and its B3LYP/6-31G(d) gas phase geometry. Calulation of the molecular volume requires the following input:

# Becke3LYP/6-31G(d) int=finegrid volume

b3lyp/6-31G(d) opt gauche-1,2-dichloroethane

0  1
X1
X2  1  1.0
C3  1  r3  2  90.0
C4  1  r3  2  90.0  3  180.0
Cl5  3  r5  1  a5  2  d5
Cl6  4  r5  1  a5  2  d5
H7  3  r7  1  a7  5  d7
H8  4  r7  1  a7  6  d7
H9  3  r9  1  a9  5  d9
H10  4  r9  1  a9  6  d9

r3=0.7581832
r5=1.80758744
r7=1.09354021
r9=1.09097562
a5=113.01671309
a7=109.01355166
a9=111.44412088
d5=34.80402243
d7=118.42989149
d9=-120.84409308

The additional output caused by the volume keyword can be found at the end of the Gaussian output file:

 Monte-Carlo method of calculating molar volume:
 based on  0.001 e/bohr**3 density envelope.
 Number of points per bohr**3 =   20 CutOff= 1.00D-04
 Using the SCF density.
 There are       379 points.  Will hold       379 in memory.
 LenV=    16741044 MDV=    16777216.
 Box volume = 6835.469 fraction occupied=0.092
 Integrated density= 1.3626292465066807D+01 error=-3.6373707534933191D+01
 Molar volume =  631.244 bohr**3/mol ( 56.332 cm**3/mol)
 Recommended a0 for SCRF calculation =  3.60 angstrom (  6.80 bohr)

Using the recommended cavity radius of 3.60 Angstroms and the gas phase geometry we can now set up the Onsager reaction field calculation for a polar solvent such as acetonitrile. Our first run will be a single point calculation using the gas phase geometry. Details of the Onsager model are specified using the SCRF keyword:

#P Becke3LYP/6-31G(d) scf=tight SCRF=(Dipole,Solvent=Acetonitrile,A0=3.60)

b3lyp/6-31G(d) SCRF gauche-1,2-dichloroethane

0  1
X1
X2  1  1.0
C3  1  r3  2  90.0
C4  1  r3  2  90.0  3  180.0
Cl5  3  r5  1  a5  2  d5     
Cl6  4  r5  1  a5  2  d5    
H7  3  r7  1  a7  5  d7
H8  4  r7  1  a7  6  d7
H9  3  r9  1  a9  5  d9  
H10  4  r9  1  a9  6  d9  

r3=0.7581832
r5=1.80758744
r7=1.09354021
r9=1.09097562
a5=113.01671309
a7=109.01355166
a9=111.44412088
d5=34.80402243
d7=118.42989149
d9=-120.84409308

The choice of the solvent can alternatively also be specified by directly giving the dielectric constant:

SCRF=(Dipole, Dielectric=36.64,A0=3.60)

The effects of the acetonitrile solution are included in the Hamiltonian in such a fashion that the mutual solute-solvent polarization is treated simultaneously with the self consistent optimization of the wavefunction. What appears in the output file after completion of the SCRF calculations are several energies that are part of the overall Onsager model:

SCF Done:  E(RB+HF-LYP) =  -999.018633476     A.U. after   12 cycles
             Convg  =    0.4543D-08             -V/T =  2.0036
             S**2   =   0.0000
 Final SCRF E-Field is:
 Dipole      :   0.00000000  0.00000000 -0.00404218
 Quadrupole  :   0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000
 Octapole    :   0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000
 Hexadecapole:   0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000
 Polarization energy = -0.267823439392E-02
 Total energy of solute =  -999.021311711
 Total energy (include solvent energy) =  -999.018633476
 Total energy (without reaction field) =  -999.015955242

These energies have to be compared to the gas phase total energy of gauche-1,2-dichloroethane at the Becke3LYP/6-31G(d) level of theory of E_tot = -999.016301783 Hartree. In the presence of the reaction field the gas phase wavefunction distorts to increase the dipole moment of the solute (from 2.9322 Debye in the gas phase to 3.3682 Debye in acetonitrile solution) and thus the interaction with the external field. The energy associated with this wavefunction is given as "Total energy (without reaction field)" and is less favorable than the unperturbed gas phase solution. Interaction of this (distorted) wavefunction with the (polarized) continuum lowers the total energy of the system to the "Total energy of solute". Accounting for the effort of polarizing the continuum one arrives at the final "Total energy (include solvent energy)". In order to obtain a complete total free energy in solution one would also have to add the effects of thermal motion of the solute.

Proceeding along the same lines for the C_2h symmetric trans-conformer in its B3LYP/6-31G(d) gas phase geometry we obtain a slightly different recommended value of 3.82 Angstroms for the Onsager cavity radius. In order to treat both conformers on equal footing the same value of 3.72 Angstroms will be used as before:

#P Becke3LYP/6-31G(d) scf=tight 
 SCRF=(Dipole,Solvent=Acetonitrile,A0=3.60)

b3lyp/6-31G(d) SCRF trans-1,2-dichloroethane

0  1
X1
X2  1  1.0
C3  1  r3  2  90.0
C4  1  r3  2  90.0  3  180.0
Cl5  3  r5  1  a5  2  -90.0
Cl6  4  r5  1  a5  2  -90.0
H7  3  r7  1  a7  5  d7
H8  4  r7  1  a7  6  d7
H9  3  r7  1  a7  5  -d7
H10  4  r7  1  a7  6  -d7

r3=0.7591126
r5=1.81475775
r7=1.0904475
a5=109.23562407
a7=111.57656952
d7=118.50082551

When comparing the results obtained for the trans-conformer in the gas phase (E_tot = -999.019007956 Hartree) with the results obtained from the SCRF calculation we face one of the limitations of the Onsager model:

 SCF Done:  E(RB+HF-LYP) =  -999.019025203     A.U. after   12 cycles
             Convg  =    0.3256D-08             -V/T =  2.0036
             S**2   =   0.0000
 Final SCRF E-Field is: 
 Dipole      :   0.00000000  0.00000000  0.00000000
 Quadrupole  :   0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000
 Octapole    :   0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000
 Hexadecapole:   0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000  0.00000000
                 0.00000000  0.00000000  0.00000000
 Polarization energy = -0.285621111172E-32
 Total energy of solute =  -999.019025203
 Total energy (include solvent energy) =  -999.019025203
 Total energy (without reaction field) =  -999.019025203

Since the Onsager reaction field model only includes the interaction between the molecular dipole moment and the reaction field, the solvation energy is exactly zero for all those systems, whose dipole moment is zero. The total energy in solution is thus identical to the total energy in the gas phase.

Still the Onsager reaction field model can be used to predict qualitatively correctly the dependence of the gauche/trans energy difference in 1,2-dichloroethane on the solvent polarity.

The particular usefulness of the Onsager reaction field model is due to the fact that gradients and second derivatives can easily be calculated and that geometry optimzations as well as frequency calculations are possible without much more effort than is required in the gas phase.

The Onsager reaction field can be put to good use when trying to reproduce the solvent dependence of the vibrational spectra of simple carbonyl compounds such as formaldehyde. The following table contains the vibrational frequencies measured in the gas phase and in acetonitrile (in cm^-1):

medium	dielectric constant	vib₁	vib₂	vib₃	vib₄	vib₅	vib₆
vapor	1.00	1167	1249	1500	1746	2782	2843
acetonitrile	36.64	-	1247	1503	1723	2797	2876

difference	-	-	-2	+3	-23	+15	+33

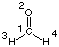These trends can be reproduced semi-quantitatively using the Onsager reaction field model in combination with Hartree-Fock theory or hybrid density function methods such as Becke3LYP and medium sized basis sets such s 6-31G(d) or 6-31+G(d).

One more interesting application of the Onsager reaction field model concerns the optimization of molecular structures that are not even stationary points in the gas phase. This is particularly usefull for strongly polarized (charge separtated) structures and the S_N2 substitution reaction of primary amines with alkyl halides (Menshutkin reaction) will be used as an example here. If we use ammonia as a simple amine and methyl chloride as the reaction partner, we should assume that the S_N2 process leads to the formation of a complex of the methylammonium cation and the chloride anion. This latter structure is, however, energetically so unfavorable in the gas phase that neither a transition state nor the product complex can be optimized.

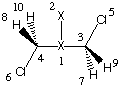
#P Becke3LYP/6-31+G(d) freq

b3lyp/6-31+G(d) opt reactant complex NH3 + MeCl

0  1
X1
C2  1  1.0
Cl3  2  r3  1  90.0
N4  2  r4  1  a4  3  180.0
H5  2  r5  3  a5  1  180.0
H6  2  r6  5  a6  3  d6
H7  2  r6  5  a6  3  -d6
H8  4  r8  2  a8  1  0.0
H9  4  r9  2  a9  8  d9
H10  4  r9  2  a9  8  -d9

r3=1.81282958
r4=3.39606276
r5=1.08870123
r6=1.08876628
r8=1.01866066
r9=1.01851992
a4=90.5440056
a5=108.63033934
a6=110.29980273
a8=111.86983212
a9=111.56759592
d6=-118.94994045
d9=-120.07441969

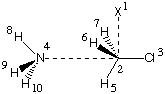However, starting from the gas phase reactant complex and using the Onsager reaction field for aqueous solution (dielectric constant = 78.39), it is possible to calculate a complete reaction profile containing the reactant and product complexes as well as the S_N2 transition state. The actual shape of the solution phase PES will, of course, depend significantly on the chosen cavity radius.

last changes: 01.04.2008, AS
questions & comments to: axel.schulz@uni-rostock.de