The Huisgen Reaction of Acetylene with Hydrazoic Acid
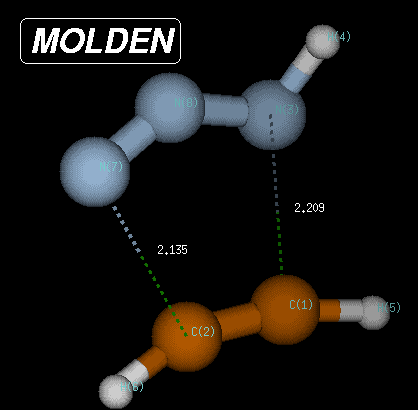
Using the Huisgen reaction (1,3-dipolar cycloaddition) of acetylene (C2H2) with hydrazoic acid (HN3) as an example, the IRC can be obtained in the following way. First locate the transition state from a suitable starting point. Using the Becke3LYP/6-31G(d) method, the transition state for this reaction has the following structure:
The transition state is characterized through C-N and C-N(H) bond distances of 2.135 and 2.209 Angstroms, respectively, and has a Becke3LYP/6-31G(d) total energy of -242.080935 Hartree. After transition state optimization, a copy of the checkpoint file containing the transition state structure is made for the IRC calculations (e.g. test1ircf.chk). From this copy, the forward IRC calculation is then initiated using the following input:
The forward IRC will be followed in this case for 20 steps with a step size of 10. The geometry is read from the checkpoint file with geom=check. Progress in these calculations can be monitored using the UNIX grep command on the string "POINTS" in the IRC output file. The number of local optimization iterations per IRC point can be monitored grep'ing on the string "STEPS". A large number of these cycles is an indication for either having a bad Hessian matrix or too large a step size. In the current example the number of optimization cycles for each of the IRC points varies between 1 and 3, a good sign for choosing a reasonable step size. This step size is, however, not large enough to complete the IRC within 20 steps and a second job with an additional 20 steps is therefore added with:
Please observe that the choice of "maxpoints" here includes the previous 20 as well as the additional 20 points. The IRC calculations continue in this particular case without any problems until step 40 is reached and can be restarted for another 20 steps to reach overall 60 steps along the IRC path. Attempted restart for another 20 points then leads to convergence problems after overall 62 steps and the job is aborted with the error message:
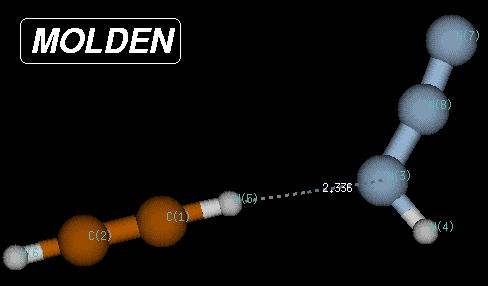
Despite this error message, Gaussian prints a summary of all points of the IRC pathway optimized before including cartesian coordinates as well as the energies. Optimization problems such as those encountered here occur frequently at the end of IRC calculations, where the potential levels off before reaching the actual product or reactant minimum. In the current case the last point on the IRC is located at C-N and C-N(H) bond distances of 3.0502 and 3.0548 Angstroms, respectively, and a Becke3LYP/6-31G(d) total energy of -242.108291 Hartree. In order to identify the remaining structural and energetic differences between the last IRC point and the following true minimum, it is good practice to optimized to the next local minimum:
In this case, the true minimum is located at a Becke3LYP/6-31G(d) total energy of -242.111452 Hartree, 80.1 kJ/mol below the transition state and 8.3 kJ/mol below the endpoint of the IRC calculations. The structure of this reactant complex is characterized through very long C-N and C-N(H) bond distances, but a short (C)H-N(H) distance of only 2.35 Angstroms. This structure shares little similarity with most of the reaction pathway and is the result of the optimization of electrostatic interactions between the two reactants.
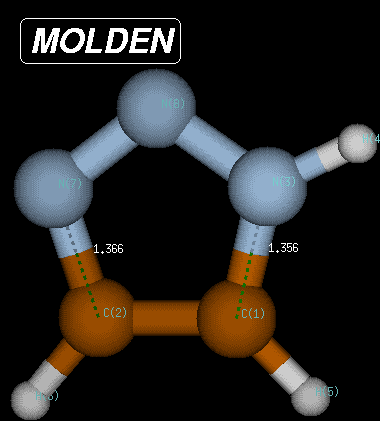
The same procedure as described above can be followed for the reverse pathway. The IRC algorithm works well for 55 points, when again the local geometry optimization does not converge anymore. At this point the structure is characterized through C-N and C-N(H) bond distances of 1.392 and 1.379 Angstroms, respectively, and a Becke3LYP/6-31G(d) total energy of -242.220156 Hartree. Reoptimization of the last point on the IRC then leads to the fully optimized product of the Huisgen reaction with a total energy of -242.222319 Hartree and C-N and C-N(H) bond distances of 1.366 and 1.356 Angstroms, respectively. The reaction product is thus 371.2 kJ/mol more favorable than the transition state and 291.1 kJ/mol more favorable than the reactant complex.
The occurence of oscillations during the constrained local optimizations are the most frequent problems encountered in IRC calculations. These oscillations can, to some extend, be avoided using smaller step sizes in combination with tighter convergence criteria. In case the IRC algorithm continues to work until the very end of the reaction pathway, the arrival at a minimum energy structure is indicated by the message:
Despite this optimistic claim, the final structure obtrained in IRC calculations may still have gradients, which are substantially larger than acccepted for true minimum energy structures. It is therefore a good practice to subject the IRC end point structures to a standard geometry optimization procedure.