Hartree-Fock Theory
In Hartree-Fock (HF) theory the energy of a system is given as a sum of five components:
EHF = ENN + ET + Ev + Ecoul + Eexch
The nuclear-nuclear repulsion ENN describes the electrostatic repulsion between the nuclei and is independent of the electron coordinates. In time-independent HF theory, the kinetic energy of the nuclei is not, but the kinetic energy of the electrons ET is considered. Together with the nuclear-electron attraction energy Ev it depends on the coordinates of one electron. The classical electron-electron Coulomb repulsion energy Ecoul and the non-classical electron-electron exchange energy Eexch depend on the coordinates of two electrons. Calculation of these last two terms constitutes the main effort in HF calculations and is also responsible for the unfavorable formal scaling of computational effort as the fourth power of basis functions used for the description of the wavefunction. The particular assumption made in HF theory is that each electron feels the other electrons only as an average charge cloud, but not as individual electrons.
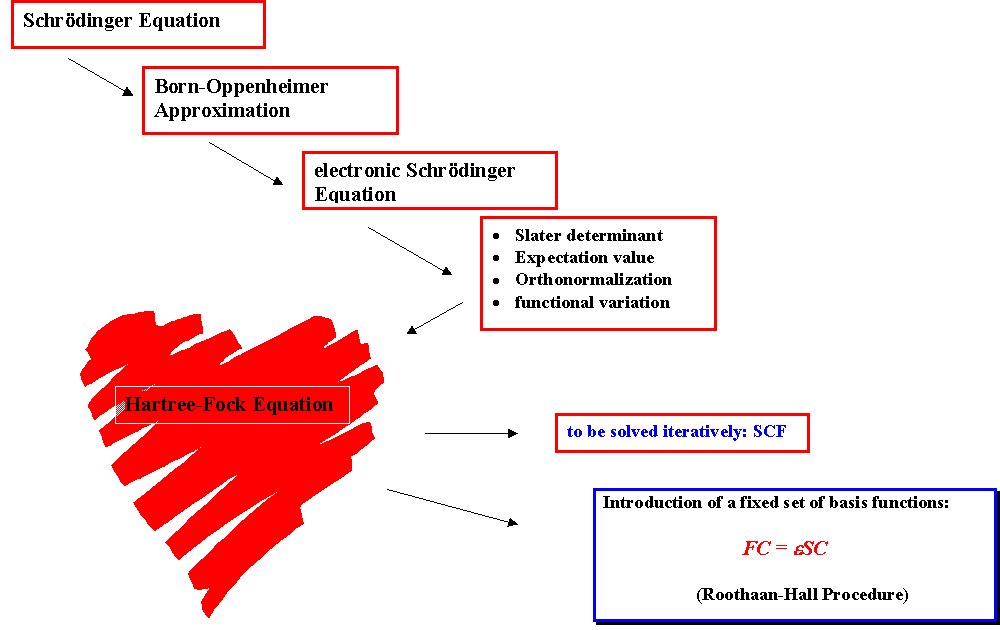
The molecular electronic wavefunction in HF theory is based on the LCAO (=linear combination of atomic orbitals) scheme describing each molecular orbital (holding one electron) as a linear combination of basis functions (usually located at the nuclear center):
The molecular orbital coefficients describe the contribution of each of the basis functions to a given molecular orbital. The overall electronic wavefunction of the system is constructed as an antisymmetrized product of the molecular orbitals (the Slater determinand) in order to fulfill the Pauli exclusion principle. Since the optimal shape of one molecular orbital depends on the shape of all the other occupied molecular orbitals, the optimization of the overall wavefunction is achieved in an iterative manner, varying the molecular orbital coefficients until no further changes in the overall wavefunction occur. The direction of the variation of MO coefficients is guided by the variational principle stating that an approximate wavefunction yields an energy of the system which is higher than the energy obtained from the exact wavefunction. In other words: in order to arrive at the most favorable wavefunction the MO coefficients must be varied such that the energy of the system becomes as low as possible.
The basic steps performed in HF energy calculations will be illustrated using formaldehyde in its C2v structure as example. Please observe that the output obtained from HF calculations will vary dramatically depending on whether normal (#) or extendet (#P) output is specified:
After reading in the geometry of the system and determining its symmetry properties, the actual first step of Hartree-Fock calculations consists in choosing a basis set in which the electronic wavefunction can be expanded. This is done in link 301 of the program, usually by calling a predefined set of basis functions from a library. In the current case we are using the standard STO-3G basis set containing three Gaussian functions (primitives) to describe each Slater-type "atomic" orbital. Sufficient basis functions are used to describe the core and valence orbitals of the system. For formaldehyde there will be one basis function for the 1s orbitals of hydrogen and five basis functions each to describe the 1s2s2px2py2pz orbitals of carbon and oxygen. Overall this amounts to 12 basis functions. As each of these basis functions is described by three Gaussian type functions, we have 36 primitive Gaussians for the system.
Aside from basis set considerations link 301 also reports the number of electrons (here 16 electrons; 8 alpha and 8 beta spin electrons) and the nuclear repulsion energy ENN in atomic units (Hartree). Subsequent links 30x (x=2,3, . . ) are responsible for the computation of one and two electron integrals.
A first guess for the wavefunction of the system is made in link 401. While earlier versions of Gaussian used the semiempirical INDO method to derive a first guess of the wavefunction, the Harris density functional method is used more recently. The orbital symmetries are printed for the occupied and the empty (virtual) orbitals.
The actual Hartree-Fock energy calculation is performed by link 502 in an iterative manner until self consistency of the wavefunction (self consistent field (SCF) calculation) is achieved. At the beginning of link 502 the convergence criteria (rms and max. density changes) are listed together with the default number of iterations (here 64). The most important information listed for each SCF cycle are the actual energy of the electronic subsystem (that is, the total energy without the core-core repulsion energy) as e.g. E= -112.352697484853, and the energy change with respect to the previous SCF iteration, e.g. Delta-E= -0.017123861810. All energies are given in atomic units.
A graphic presentation of the optimization procedure is given here.
At convergence the total energy (now including the core-core repulsion energy) is reported as E(RHF) together with the number of SCF cycles required to reach convergence (here 9), the ratio of kinetic to potential energy -V/T , the electronic kinetic energy ET as KE, the electron-nuclear attraction energy Ev as PE, and the sum of Coulomb and exchange interaction energies Ecoul + Eexch as EE. Further information on the converged wavefunction is given by link 601:
This entails the symmetries of occupied and virtual orbitals (which may or may not be identical to the symmetries listed for the wavefunction guess), the symmetry of the electronic state of the system, orbital energies of all orbitals (in Hartree), and essential results from a Mulliken population analysis. The components of various multipoles (dipole, quadrupole . . ) are given at the end.
For more theoretical details (lecture) click here.