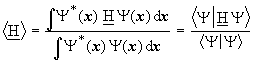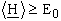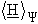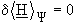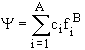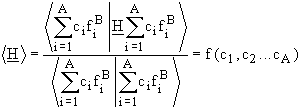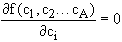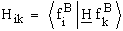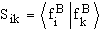An important principle in quantum mechanics, the variation principle, states that the more flexible the wave function, the lower the energy and, which in turn implies, the better the wave function. Zero on the energy scale has all particles separated at infinity. Calculated energies are thus negative numbers, the larger the number the lower the energy. As already indicated, the Schrödinger equation for a multi-electron system is insoluble. The variation principle, however, results in approximate solutions. For example, to determine the total energy of a stationary system, the expectation value of the energy

can be worked out according to the postulates of quantum mechanics as follows:

where Y is any arbitrary trial-function. (If the trial-function, Y , corresponds to an eigenfunction of the Schrödinger equation, then the expectations value of the energy equals the energy eigenvalue, E0, calculated from the Schrödinger equation.) IfE0 is the exact energy of the ground state of a system, and thus corresponds to the exact solution of the Schrödinger equation, it can be proven that the expectation value of any trial-function, Y , is always equal to, or larger than E0:

* This only applies to the total energy. Relative energies can be greater or less than the exact D E!

Thus, in a variational calculation, the above inequation serves as a reference for the accuracy of the wave function obtained. Since E0 is the minimum energy of the system, the lowest expectation value

is sought. This means that a wave function must be found which minimizes the expectation value:

In practice, it is often useful to linearize this variational problem by approximating the wave function with a linear combination of a fixed set of basis function (finite number, A):

In doing this the variational parameters ci are introduced:

Solving the system of partial derivatives:

leads to a generalized matrix eigenvalue problem (the so-called secular equations, written as a matrix):

Hc = eSc

Here, the coefficient vector

c= (C₁ ... C_A),

H=(H)ik

and

and the overlap matrix

S = (S)ik

and

e represents the matrix of the eigenvalues. The smallest eigenvalue corresponds to the optimized e[Y ].